当前位置：知识库 > 技术贴 > 优化方法发展现状

优化方法发展现状

来源： 2023-03-27 rootadmin

优化的应用非常广泛，甚至可以说无处不在。那么，作为支撑的优化方法，发展到了什么程度了？

这可以用一张图来概括（如下图）。

null

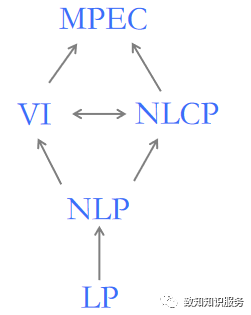
从下到上，难度逐渐增大。

线性规划（Linear Progarmming, LP），已经有了单纯形法和内点法，可以认为是彻底解决了的问题。

非线性优化（Non-Linear Programming, NLP），对于定义在凸集上的凸函数可以解。除此以外，若优化模型中含有特殊结构，如锥等，也是可解的。对任一个非凸的非线性规划，尚无一般解法，即使是一个二次的单目标，两个非凸的二次约束也没有通用解法。但对给定的NLP问题可以用NLP优化的基本思想和手法去设计解法，即需要具体问题具体分析。

再难一点是变分不等式（Variational Inequality Problem, VI）和非线性互补问题（Nonlinear Complementarity Problem, NLCP）。这二者的难度相同，主要是求解均衡问题。

最上面的是带均衡的数学规划（Mathematical Programming with Equilibrium Constraints, MPEC），是在均衡基础上求最优解。如交通流的优化问题。

优化与实际密切相关，以上都是从实践中提炼出来的问题。若任意设定一个优化问题，则会有更难以求解的问题，但不见得有实际意义。

综上，尽管有很多关于优化的知识，但我们对优化仍知之甚少，优化方法仍需发展。优化方法目前只能讲到LP和NLP。也就是说，当系统地学习了LP和NLP，就来到的优化领域的前沿。

- END -